Szsz.pl: Najdłuższy dzień w roku

Najdłuższy dzień w roku

poniedziałek, 21 czerwca 2010

Dziś jest najdłuższy dzień w roku.

Ponieważ ten dzień zawsze był dla mnie w jakiś sposób szczególny, chciałem by również ta strona wzbogaciła się o coś specjalnego. Wpadłem na pomysł by wygląd strony odzwierciedlał porę dnia i tu pojawił się dziwaczny problem.

Poszukiwania

Jak łatwo zgadnąć, zacząłem od poszukiwań gotowego rozwiązania, lub wzoru…

Jednak… Na jakimś forum trafiłem na wypowiedź dzieciaka twierdzącego że czegoś podobnego nie da się wyliczyć… Osłupiałem… W epoce, gdy ludzie wysyłają automatyczne sondy na wieloletnie misje po całym układzie słonecznym, ktoś twierdzi że nie da się wyliczyć położenia słońca na niebie? To niby jak przez stulecia żeglarze ustalali swoje położenie?

Wygląda na to że lata bez obowiązkowej matematyki na maturze zrobiły swoje.
Nigdy nie byłem orłem, ale coś takiego jeszcze potrafię policzyć…

Rozgrzewka

Na początek, coś na poziomie szkoły podstawowej…

Cofnijmy się na chwilę do 23 marca, do równonocy wiosennej. Gdybyśmy wtedy byli w okolicach równika, Słońce świeciło by na nas pionowo z góry. Szybki skok na biegun i tam Słońce znajdowało by się dokładnie na horyzoncie.

Mamy więc pierwszy element układanki:

sun_max(lat) := 90° - |lat|

Wracając do dnia dzisiejszego…

Ziemia jest nachylona względem słońca pod kątem 23.45° i o tyle zmienia się położenie słońca.

sun_max(lat) := 90° - |lat - 23.45°|

Używając tego prostego wzoru, można już wyliczyć jak wysoko było dziś Słońce w południe. Dla południowej polski będzie to 63.45°

Założenia

Żeby posunąć się nieco dalej, warto przyjąć pewne założenia, które uproszczą dalsze obliczenia.

Na pierwszy ogień musi pójść nasz nieszczęsny kalendarz, w którym rok dzieli się na 12 miesięcy, liczących od 28 do 31 dni, dających w sumie 365 lub 366 dni, podzielonych na 24 godziny, które są podzielone na 60 minut… Takie coś nadaje się do zaznaczania dnia w którym odwiedzi nas Święty Mikołaj, wchodząc przez kaloryfer, ale nie udzieli nawet odpowiedzi za ile dni to nastąpi.

Idealna wydaje się Data Juliańska. Żeby nie komplikować: dziś jest dzień zerowy. Południe będzie godziną zero. (Jeśli ktoś uważa to za dziwaczne: Po drugiej stronie Ziemi jest wtedy środek zimy i północ). Dodatkowo, nie przyjmuję założeń co do związku pomiędzy długością dnia i roku.

Kolejne uproszczenie, wynika z mojego lenistwa. Zamiast podawać kąty w radianach, wolę używać liczby z zakresu 0..1. Jedyne o czym trzeba pamiętać to by używać funkcji cosinus w taki sposób: cos(2π α).

Podsumowując


DEG:  1/360;  /* stopnie */
YEAR: 365.25; /* ile dni ma rok */
DAY:  1/YEAR; /* długość dnia w latach */
HOUR: 1/24;   /* długość godziny w dniach */
axis: 23.45*DEG; /* kąt nachylenia ziemi */

Położenie Słońca w południe

Wracając do wzorów. Żeby wyliczyć położenie Słońca w południe, o dowolnej porze roku, wystarczy ustalić jak zmienia się nachylenie Ziemi (deklinacja):

decl(day) := axis * cos(2π * day)

Wcześniejszy wzór wygląda teraz tak:

sun_max(lat, decl) := 90° - |lat-decl|

Kod, w JavaScript, będzie wyglądał tak:

var DEG = 1/360;
var axis = 23.45*DEG;
function decl(day) { return axis * Math.cos(2*Math.PI * day); }
funciton sun_max(lat, decl) { return 0.25 - Math.abs(lat - decl); }

Sprawdźmy, za pół roku w przesilenie zimowe Słońce będzie na wysokości 16.54°
(sun_max(50*DEG, decl(0.5)) / DEG)

OK, działa

Wschody i zachody słońca (równonoc)

Pora na opisanie ruchu dziennego słońca.

Wracając na chwilę do równonocy, położenie Słońca na równiku będzie opisywała funkcja: 90° * cos(2π * h*HOUR), natomiast na biegunach taka: 0°. U nas wysokość Słońca będzie wartością z zakresu -40° do 40°.

sun_day(lat, h) := 90° - |lat| * cos(2π * h)

Mamy więc funkcję, która opisuje całe dwa dni w roku…
(bez uwzględnienia deklinacji)

Złożenie wzorów

Pozostaje tylko poskładać razem dwie funkcje sun_max i sun_day

Pierwsza z nich opisuje zmiany położenia Słońca w roku, druga zmiany dzienne. W chwili zerowej obie funkcje dają ten sam wynik. Konieczne jest przesunięcie wyników sun_day, tak by uzyskać różnice wzgledem tej chwili…

sun_day(lat, h*HOUR)-sun_day(lat,0)

… i można zsumować obie funkcje

sun_max(lat, decl(day)) + sun_day(lat,hour) - sun_day(lat,0)

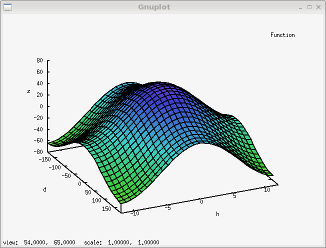
… upraszczając:

sun_ang(lat, day, hour) := 
    sun_max(lat, decl(day)) +
    sun_day(lat,hour) +
    |lat| - 90°

… mamy nieomal gotowe rozwiązanie.

Położenie Słońca o dowolnej porze dnia i roku

Na koniec pozostał opis relacji pomiędzy ruchem obrotowym Ziemi wokół Słońca, a obrotem wokół osi i uproszczenie wzorów.

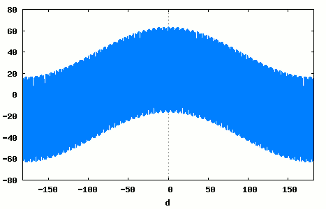
… i jest rozwiązanie:

sun(lat,day) := - |axis * cos(2π * day/year) - lat|
                + |lat|
                + cos(2π * day) * (1/4 - |lat|)

Uproszczenia przeprowadziłem używając programu Maxima

Dla przypomnienia: axis = 23.45/360, year = 365.25. Dni są liczone od 21 czerwca 2010. Godziny są częścią ułamkową dnia. Wszystkie miary kątowe wymagają przeliczenia na liczbę z zakresu 0..1

function sun(lat, day) {

 var PI = Math.PI;
 var cos = Math.cos;
 var abs = Math.abs;

 lat /= 360;

 var angle = abs(lat)
  - abs(23.45/360 * cos(2*PI * day/365.25) - lat)
  + cos(2*PI * day) * (0.25 - abs(lat));

 return angle * 360;
}

Czy wzór jest dokładny? W miarę… Porównałem kalendarzem, wygląda na to że nie ma błędów. Jednak, wszystkie stałe zostały podane w przybliżeniu. Mało tego, wyliczając godzinę wschodu i zachodu warto pamiętać że Słońce nie jest punktem i ma średnicę około 0.5°, natomiast nasza atmosfera sprawia że będzie ono widoczne 6° poniżej linii horyzontu.

Na koniec

No i mam wzór, ale nie zrobiłem tego co chciałem. Są lepsze sposoby spędzania najdłuższego dnia w roku, niż siedzenie przy komputerze. Cóż… może następnym razem?

Pozostaje tylko mieć nadzieję że moje wyliczenia komuś się przydadzą.

Etykiety: B, G, R, wzory

Red 23:11

Szsz.pl